evolutas e involutas

contacto

eduardo.veloso@mac.com

Temas de geometria

Curvas notáveis

Evoluta e Involuta

Por <a href="//commons.wikimedia.org/wiki/User:Sam_Derbyshire" title="User:Sam Derbyshire">Sam Derbyshire</a> - <a class="external free" href="https://en.wikipedia.org/wiki/File:Evolute1.gif">http://en.wikipedia.org/wiki/File:Evolute1.gif</a>, CC BY-SA 1.0, Hiperligação

https://commons.wikimedia.org/wiki/File:Evolute1.gif#/media/Ficheiro:Evolute1.gif

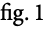
Consideremos uma curva plana, por exemplo uma elipse (a vermelho na figura). Seja P um ponto da elipse e adoptemos a definição de Cauchy para centro de curvatura (da elipse) no ponto P: ponto de intersecção de duas rectas normais à curva e infinitamente próximas de P. Na figura as rectas finas a azul são normais à elipse e cada uma delas contém um ponto P da elipse e um ponto C —centro de curvatura correspondente. O conjunto dos centros de curvatura forma a figura a azul, a traço grosso, que se designa por evoluta da elipse. Note-se que a definição actual de evoluta é dada em termos de geometria diferencial, mas aqui utilizamos, tendo em atenção os leitores a que dedicamos este texto, uma linguagem mais amplamente compreendida. Se uma curva a é a evoluta de uma curva b, então b é definida como involuta de a. Assim, a elipse (a vermelho) da fig. 1 é a involuta da curva azul a traço grosso. Nas páginas relativas à ciclóide iremos mostrar como estes conceitos se aplicam nesse caso.

..